티스토리 뷰
1. 시계열(Time series) 데이터란?
- 시간에서 순차적으로 (sequentially) 관측한 값들의 집합
- 독립변수(Independent variable)를 이용하여 종속변수(Dependent variable)를 예측하는 일반적인 기계학습 방법론에 대하여 시간을 독립변수로 사용한다는 특징
- 독립변수로 시간을 사용하는 특성때문에 분석에 있어서 일반적인 방법론들과는 다른 몇가지 고려가 필요
2. 시계열 자료 분석 방법
- 일변량 시계열 분석 - {Yt ; t = 1,2,..,T}만을 가지고 분석
- 회귀분석(계량경제) 방법, BOX-JENKINS 방법
- 수학적 이론 모형에 의존하고 시간에 따라 변동이 많은 (빠른) 시계열 자료에 적용
- 회귀분석(계량경제) 방법, BOX-JENKINS 방법
- 지수 평활법, 시계열 분해 방법
- 다소 직관적인 방법이며 시간에 따른 변동이 느린 데이터를 분석하는데 사용
- 다중 시계열 분석 - {Yt ; t = 1,2,..,T}와 설명변수(입력) {Xt ; t = 1,2,..,T} 가 있는 경우
- 회귀모형(계량 경제 모형)
- 전이함수 모형(Transfer function model)
- 개입분석(intervention analysis)
- 상태공간분석(State space analysis)
- 다변량 ARIMA 모형
3. 정상 확률 과정과 비 정상 확률 과정
3.1 정상 확률 과정
- 협의의 정상 확률 과정(strictly stationary process, strong stationary process)
- 확률 과정의 모든 모멘트(moment)가 시간 차이(time lag)에만 의존하고 절대 시간에 의존하지 않는 것
- 자기상관계수 함수(auto-correlation function) 줄여서 ACF
- 시간이 지나도 신호의 확률적 특성이 그대로 유지되는 확률 과정
- 시간의 추이와 관계없이 평균 및 분산이 불변하거나 시점간의 공분산이 기준 시점과 무관한 형태의 시계열
# stationarity check
(1) 눈으로 직관적 확인 ~ STL, Rolling statistics(moving average)
(2) Dickey-FUller test
- 시계열 모델을 분석하고 예측하기 위해서는 정상적 조건이 확보되어야함
- 1979년 David Dickey와 Wayne Fuller 가 고안안 검정법


3.2 비정상 확률 과정
- 시계열이 안정적이지 않을 때에는 로그를 이용하거나 차분을 통해 시계열을 안정적으로 변환한 뒤에 분석 시행

4. 시계열 데이터 요소
- 추세(Trend): 장기적으로 나타나는 변동 패턴
- 계절성(Seasonal): 주,월,분기,반기 단위 등 이미 알려진 시간의 주기로 나타나는 패턴
- 주기(Cyclic): 최소 2 년 단위로 나타나는 고정된 기간이 아닌 장기적인 변동
- 랜덤요소 (random/residual/remainder)


5. 시계열 데이터 Model
- 비정상 과정 모형 중 가장 대표적인 것은 ARMA 모형을 누적한 ARIMA(auto-regressive integrated moving average) 모형
- ARIMA 모형은 과거 지식이나 경험을 바탕으로 한 행동에 따라 시계열이 움직이고 있음을 기초로 하는 것.
- 과거의 관측값과 오차를 사용해서 현재의 시계열 값을 설명
- ARMA(Auto-regressive Moving Average)일반화 한것 -> Stationary Series 에만 적용
- ARIMA-> Non stationary series 적용가능
- Autoregressive : 자기회귀모형
- Moving Average : 이동평균모형
- 자기 회귀와 이동 평균을 고려하는 모형
- 시계열의 비정상성(Non-stationary)을 설명하기 위해 관측지간의 차분(Difference)을 사용한다는 차이점이 있음
- 규칙성을 만드는 패턴
- 자기상관성(Autocorrelativeness) - 이전의 결과와 이후의 결과 사이에서 발생하는 현상
- 이동평균(Moving Average) - 이전에 생긴 불규칙한 사건이 이후의 결과에 편향성을 초래하는 이동현상
- White Noise
- 많은 수계열 모형들이 불규칙한 패턴
- 평균이 0이며 일정한 분산을 지닌 정규분포에서 추출된 임의의 수치라고 규정
- 정규분포 가정은 모델의 해석을 전반적으로 편리하게 만들기 때문에 대부분의 통계 및 수리분석에서 채택
- 회귀식에서 설명되지 않은 ERROR의 의미와 유사
- = Uncontrolable variable
5.0. 자기상관모형 -AR
- 자기 상관이란 Random Variable에 대해서 이전의 이후값이 영향을 미치고 있는 상황 이야기
- 예를 들면 이전에 값이 크면 이후에는 낮은값이 나온다는 경향
- 자기 상관성을 시계열 모형으로 구성한 것을 AR 모형이라고 부름
5.1 이동평균 - MA 모형
- 시간이 지날수록 Random Variable의 평균값이 지속적으로 증가하거나 감소하는 경향이 생길 수 있음
5.2 ARMA 모형
- AR모형과 MA모형을 합친것
5.3 ARIMA 모델의 모수 의미

- 현실에 존재하는 시계열 자료는 불안정(Non-stationary)한 경우가 많다
- AR(p), MA(q) 모형이나 이 둘을 합한 ARMA(p,q)모형으로는 이러한 불안정성을 설명할 수 없다.
- 이러한 비 정상성을 제거하는 과정을 포함한 것이 ARIMA 모형이며 ARIMA(p,d,q)로 표현
- + 과거의 데이터가 지니고 있던 '추세 Momentum'까지 반영하게 됨
- Correlation뿐만 아니라 Cointegration까지 고려한 모델
- ARIMA의 모수는 크게 3가지
- AR모형의 Lag을 의미하는 p, MA모형의 Lag을 의미하는 q, 차분(Diffrence)횟수를 의미하는 d
- 보통은 p, d, q의 순서
- p + q < 2, p * q = 0 → p나 q 두개 중 하나는 0이라는 이야기
- 시계열 자료에서는 하나의 경향을 띄기 때문에, 이렇게 사용하는 것이 더 잘 맞다
5.3.1 p와 d, q 는 어떻게 정의할까?
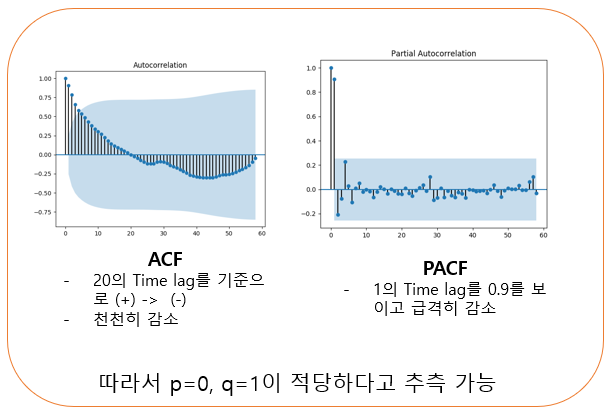
- ACF plot와 PACF plot을 통해 AR 및 MA의 모수를 추정
- ACF(Autocorrelation function)
- Lag에 따른 관측치들 사이의 관련성을 측정하는 함수

- PACF(Partial autocorrelation function)
- k 이외의 모든 다른 시점 관측치의 영향력을 배제하고 y_k와 y_(k-1) 두 관측치의 관련성을 측정하는 함수

- AR의 특성 - ACF는 천천히 감소하고 PACF는 처음 시차를 제외하고 급격히 감소 (0,1)
- MA의 특성 - ACF는 급격히 감소하고 PACF는 천천히 감소 (1,0)
- 급격히 감소하는 시차를 각 AR과 MA 모형의 모수(p, q)로 사용
- 데이터를 차분하여 ACF 및 PACF 계산함으로써 적절한 차분횟수까지 구할 수 있음
<출처>
1. 스택익스체인지
Stationarity Tests in R, checking mean, variance and covariance
This question was first asked on Stackoverflow, but as no one was able to answer, I wanted to ask it here. The question is: is there a test for stationarity that is both able to identify stationar...
stats.stackexchange.com
2. 네이버 블로그
'인공지능 > 머신러닝' 카테고리의 다른 글
| [ML Algorithm] Gradient Boosting Machine (0) | 2019.10.15 |
|---|---|
| [ML Algorithm] 랜덤포레스트(Random Forest) (0) | 2019.10.15 |
| [ML Algorithm] 결정트리모델(Decision Tree Model) (0) | 2019.10.15 |
| [ML Algorithm] 앙상블 방법(Ensemble Method) (0) | 2019.10.14 |
| [ML Algorithm] label encoding 과 one hot encoding (0) | 2019.10.06 |
댓글
