티스토리 뷰
1. 신경망
- 인공신경망? 1943년 신경 생리학자 워런 맥컬록과 수학자 월터 피츠가 이를 처음 소개
- 명제논리를 사용하여 동물 뇌의 생물학적 뉴런이 복잡한 계산을 위해 어떻게 상호작용하는지에 대한 간단한 계산 모델 제공 -> 최초의 인공 신경망 구조
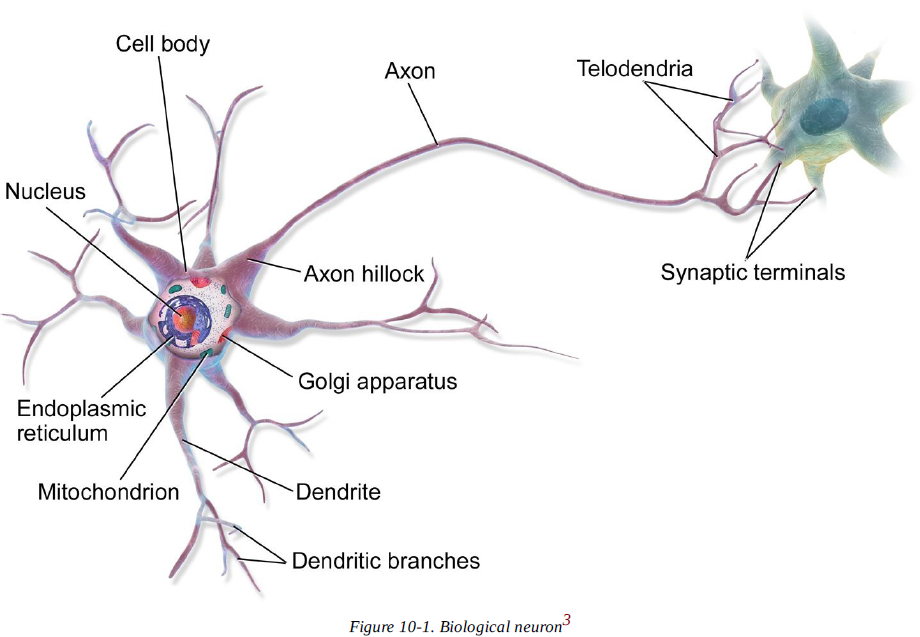
- 생물학적 뉴런은 대부분 동물의 대뇌피질( 예를 들면 우리의 뇌)에서 발견되며 핵을 포함하는 세포차와 세포의 복잡한 구성요소로 이루어져 있다.
- 수상돌기(dendrite) : 나뭇가지 모양의 돌기
- 축삭돌기(axon) : 나뭇가지 모양의 축삭 돌기
- 축삭돌기의 끝은 축삭끝까지(telodendria)라 불리는 여러 개의 가지로 나뉘고, 이 가지의 끝은 시냅스 말단(synaptic terminals)이라 불리는 미세한 구조이고 다른 뉴런의 수상돌기와 (또는 세포체에 직접)연결되어 있다.
- 생물학적 뉴런은 이런 시냅스를 통해 다른 뉴런으로부터 짧은 전기 자극 신호(signal) 을 받는다.
- 한 뉴런이 천분의 몇 초 동안 다른 뉴런으로부터 충분한 횟수의 신호를 받으면 자체적인 신호를 발생시킨다.
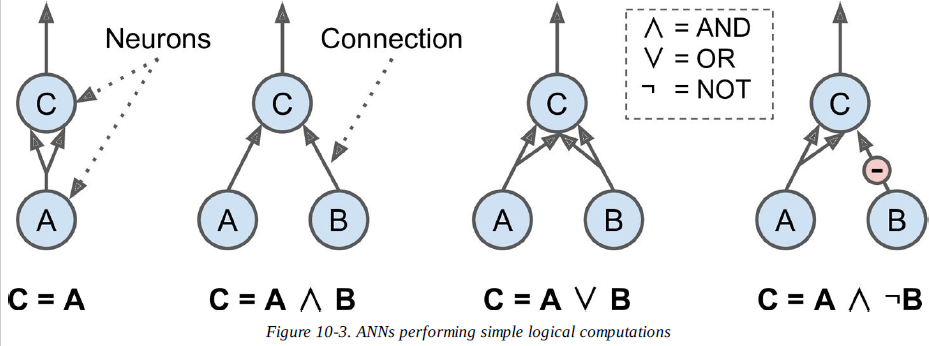
2. 뉴런을 사용한 논리연산
3. 퍼셉트론
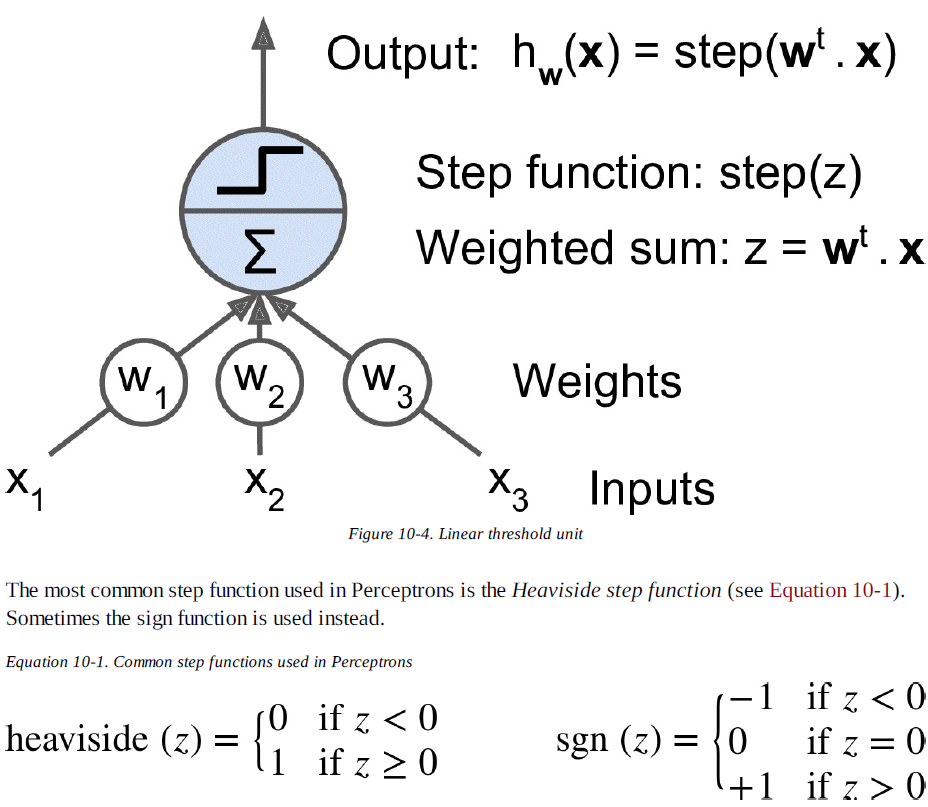
- 1957년 프랑크 로젠 블라트가 제안, 가장 간단한 인공 신경망 구조 중 하나, 신경망의 초기 연구과정 중 1950년대에 제안된 것
- 맥컬록-피츠 모델을 기반으로 두는 학습기계
- TLU(threshold logit unit)라는 조금 다른 형태의 인공 뉴런을 기반으로 함.
- 입력과 출력이(이진 on/off) 어떤 숫자고 각각의 입력 연결은 가중치와 연관이 있다.
- 퍼셉트론 프로그램의 학습 알고리즘? 헵의 법칙을 적용해 출력 값에 따라 플러스와 마이너스로 진동하도록 가중치를 업데이트
- 퍼셉트론은 네트워크가 만드는 에러를 반영하도록 조금 변형된 규칙을 사용하여 훈련된다.
- 퍼셉트론의 경우 각 출력 뉴런의 결정 경계는 선형이므로 퍼세
- 헵의 법칙? 생물학적 뉴런이 다른 뉴런을 활성화 시킬 때 이 두 뉴런의 연결이 더 강해진다. = 서로 활성화되는 세포가 서로 연결된다.
- 두가지 종류의 상태를 긍정과 부정적인 예로 설정해 출력값에 긍정적인 예라면 플럿, 부정적인 예라면 마이너스로 가중치를 업데이트
- 단순 퍼셉트론 -> 퍼셉트론 수렴 정리(perceptron convergence theorem)
>> 긍정적인 예와 부정적인 예에서 학습 데이터를 선형 분리할 수 있다면 반드시 유한한 횟수를 반복 실행해 평면 분리 상태를 찾을 수 있다는 개념
>> 그러나 데이터를 선형 분리할 수 없으면 퍼셉트론 학습을 적용할 수 없다.
>> 선형 분리할 수 있더라도 평면 분리 상태로 만드는데 상당한 시간이 걸린다.
4. 맥컬록-피츠(McCulloch-Pitts) 모델
- 1943년 Warren McCulloch, Walter Pitts에 의해 제안된 모델
- 인간의 두뇌를 논리적 서술을 구현하는 이진 원소들의 결합으로 추측, 이진 원소인 뉴런은 on이나 off 상태를 나타낸다.
- 초기 신경 시스템 모델
- 신경세포(뉴런) -> 다른 신경 세포에게 전기 신호를 받았을 때 전기 신호가 일정 기준을 넘으면 다음 신경 세포로 신호를 전달 -> 이 현상을 수학적 모델로 고안한 것이 신경망의 개념
- 실제 신경세포끼리는 시냅스라는 부위를 통해 신경 전달 물질 이동
- 받는 쪽 신경 세포의 세포막 안팎에 미세한 전위차를 발생시키며 전기신호로 시각화
- 형식 뉴런 formal neuron(소자) <- 맥컬록-피츠 모델로 고안된 신경 세포의 연결 모델
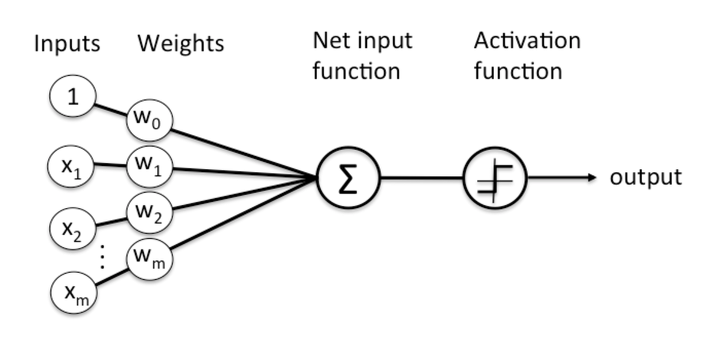
|
햅의 법칙(Hebb) - 시냅스를 통한 신경 세포의 상호작용이 증가하면 시냅스가 더 견고하게 강화되며, 상호작용이 감소하면 시냅스는 약해져 신경회로를 사용하지 않게 된다는 이론 - ‘서로 활성화되는 세포가 서로 연결된다’ - 즉 두 뉴런이 동일한 출력을 낼 때마다 그들 사이의 연결 가중치가 증가한다. |
- 신경세포의 연결에 더 견고하면 기억력 향상과 운동 능력 습득 같은 학습 작용에 도움을 준다
- 수학개념으로 바꾸면 형식 뉴런에 헵의 법칙을 적용했을 때 입력값과 출력값에 의해 가중치가 변한다.
5. 퍼셉트론 - 붓꽃예제
- 퍼셉트론의 성질
- 클래스 확률을 제공하지 않는다.
- 고정된 임곗값을 기준으로 예측 >> 로지스틱 회귀 선호
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
import numpy as np
from sklearn.datasets import load_iris
from sklearn.linear_model import Perceptron
iris = load_iris()
X = iris.data[:,(2,3)] #꽃잎의 길이와 너비 #(2,3) 2열, 3열 데이터만 추출
y = (iris.target == 0).astype(np.int) # is this Iris Setosa? #iris.taget == 0은 맨 처음 Setosa를 말함
per_clf = Perceptron(random_state = 0)
per_clf.fit(X,y)
y_pred = per_clf.predict([[2,0.5]])
print(y_pred)
|
cs |
'인공지능 > 머신러닝' 카테고리의 다른 글
| [Math] 수학이야기 - Eigenvalue와 Eigenvector가 왜 중요할까 (0) | 2019.10.16 |
|---|---|
| 머신러닝 알고리즘 - 기저함수(basis function) (0) | 2019.10.16 |
| [ML Algorithm] 인공지능 - 유전 알고리즘 (0) | 2019.10.16 |
| 그래프 이론 (1) | 2019.10.16 |
| [ML Algorithm] 머신러닝(Machine Learning) 기본 이론 (0) | 2019.10.16 |
댓글
