티스토리 뷰
1. 그래프
- 점과 선을 연결한 것
- 점 = 꼭지점 = node = vertex
- 그래프는 정점끼리 연결되어 있으면 정점이 어느 위치에 있는지는 관계가 없다.
- 따라서, 겉보기에는 다른 그래프도 정점이 이동한다면 같은 그래프가 될 수 없다. <- 이러한 그래프를 동형이라고 한다.

2. 무향 그래프와 유향 그래프
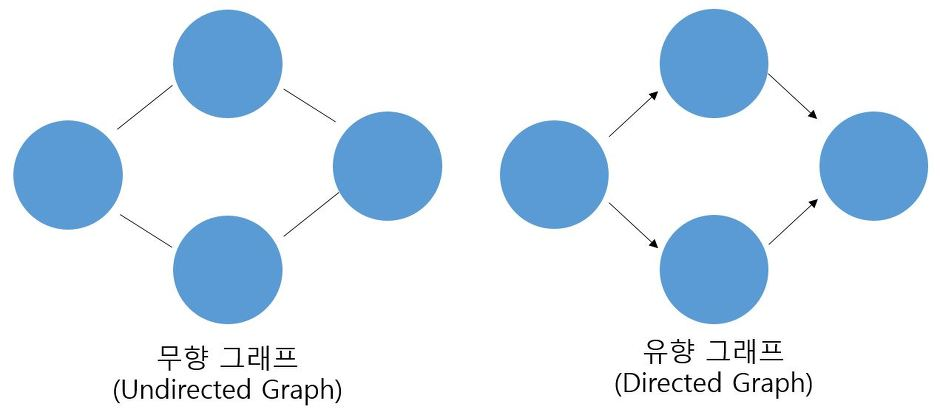
- 유향그래프(Directed Graph) : 그래프의 변에 방향이 존재하면 유향 그래프라고 한다.
- 유향 비순회 그래프(Directed Acyclic Graph, DAG) : 어떤 정점에서 출발 한 후 해당 정점에 돌아오는 경로가 하나인 그래프
- 가중 그래프(Weighted Graph) = 네트워크 : 유향 그래프 중 가중치 정보가 추가 된 그래프, 변에 가중치를 적어 가중치를 표현. 변에 숫자를 적는 것 외에 선의 굵기로 가중치를 나타낼 수도 있다.
3. 그래프의 행렬 표현
- 그래프는 여러가지 형태로 나타낼 수 있으며 그 중 행렬로 나타내는 방법이 있음
- 인접행렬(adjacency matrix) : 정점 사이의 관계를 나타내는 행렬
- 정점 수가 n일 때 nxn 행렬이며 정점 사이가 변으로 연결되어 있으면 1, 연결되어 있지 않으면 0
- 근접행렬(incidence matrix) : 정점과 변의 관계를 나타내는 행렬
- 변 수가 m때 nxm 행렬이며 정점과 변이 연결되어 있다면 1, 정점과 변이 연결되어 있지 않으면 0
- 변에 가중치가 있는 그래프라면 인접 행렬 요소를 0과 1이 아니라 가중치 값으로 구성
4. 트리 구조 그래프
- 그래프에 있는 여러 개의 정점에서 출발점이 되는 정점으로 돌아가는 경로 유일
- 트리구조 : 출발점이 되는 정점이 막다른 장점(더는 새로운 변을 통해 이동할 수 없는 정점)인 그래프
- 루트(Root, 뿌리) : 출발점이 되는 정점
5. 그래프 탐색과 최적화 - 탐색 트리 구축
- 트리 구조 그래프? 보통 출발점이 도는 정점(혹은 최초의 상태)에서 다른 정점을 향해 나아가는 보습(나무 모양 그림, 계통 나무 그림)을 통해 여러가지를 선택할 수 있는 상태를 나타냄
- 출발점에서 여러 개 종착점 혹은 여러 개의 출발점에서 하나의 종착점으로 가는 경로를 탐색하는 경우에 사용하면 좋다.
- 출발점에서 목적지를 노드(탐색트리의 정점)로 구성한 후 분기를 이용해 상태 선택
- 탐색 결과를 기반으로 트리 분기의 다음 노트 선택시? 여러 개 노드의 평가값을 계산하여 최적 경로를 찾는다
- Ex) 대중교통 환승? 출발점에서 목적지까지 도착하는 다양한 대중 교통 수단을 이용했을 때의 최소 이동시간, 최소 환승 횟수, 꼭 지나는 중간지점, 환승 요금 -> 모두 비용이 비용을 평가값으로 환산해 최적 경로를 찾는데 활용
- 최적 경로 탐색? 현재 시각 t에 해당하는 상태에 어떤 행동을 했을 때 얻을 수 있는 이익이나 지불 비용을 계산해 다음 시각인 t+1인 상태를 결정하는 것과 같다.
- 이 과정을 반복 실행하면 목적지에 도달했을 때 시간인 T의 이익을 최대화하거나 비용을 최소화하는 계획 문제로 다룰 수 있다. <다단계 (의사) 결정 문제>
6. 트리 구조
6.1 탐색 트리 추적 방법
- 막힌 지점이 있는 미로나 탐색 트리의 경로를 도달하는 목표 지점까지의 경로를 미리 파악할 수 있으면 어느 방법이 더 효율적일지 명확할 것이다.
- 목표지점은 해당 노드의 상태 평가값( ex: 승부의 포석, 막다른 노드나 목적지, 점수 등)과 이를 계산하는 평가 함수로 결정
1. 깊이 우선 탐색(Depth-first search, DFS)
- 루트 노드에 연결된 경로 중 하나를 선택해 막다른 노드에 도착할 때까지 일단 탐색한 후, 다시 바로 앞 노드로 이동해 다음 막다른 노드까지 탐색 반복
2. 너비 우선 탐색(Breadth-first search. BFS)
- 루트 노드와 연결된 노드를 모두 탐색한 다음 바로 다음에 깊이의 노드들을 전부 탐색하는 과정을 반복
- 탐색 트리의 탐색에 필요한 목록
- 탐색 대상 노드와 연결된 주변 노드를 포함하는 탐색 노드의 목록
- 오픈 리스트(open list)
- 탐색을 종료한 노드의 목록
- 클로즈드 리스트(closed list)
- 클로즈드 리스트에 도달 목표노드가 포함되면 탐색 종료
- 효율 좋은 탐색 방법
- 깊이 우선 탐색과 너비 우선 탐색은 탐색하는 노드를 순서대로 처리할 뿐이므로 더 효율적인 탐색 방법을 고민해야 처리 시간을 단축 가능
1. 비용에 따른 탐색 방법
2. 게임 트리를 전략에 이용하는 방법
'인공지능 > 머신러닝' 카테고리의 다른 글
| 머신러닝 - 신경망(퍼셉트론) (0) | 2019.10.16 |
|---|---|
| [ML Algorithm] 인공지능 - 유전 알고리즘 (0) | 2019.10.16 |
| [ML Algorithm] 머신러닝(Machine Learning) 기본 이론 (0) | 2019.10.16 |
| 머신러닝 알고리즘 - 서포트 벡터 머신(Support Vector Machines) (0) | 2019.10.16 |
| 머신러닝 알고리즘 - XGBoost(eXtreme Gradient Boosting) (1) | 2019.10.15 |
댓글
