티스토리 뷰
csv 데이터 - 10599863_0_sigma_scale1.csv

우선 이 코드에서 fft는 두가지로 나뉘어 진다.
fft_class class에서 def_fft와 def_fft_plot은 세트이다.
def_fft에서 sampling 숫자가 달라도 normalization이 가능하다. 그렇기 때문에 20 sampling 데이터와 40 sampling data라도 x축 값이 다 같게 나온다.
하지만 비교를 하기 위해서 fft_total_data은 그냥 fft data를 넣기 때문에 20 sampling 과 40 sampling 둘다 x축 값이 다 다르게 나온다.
결론: 그러므로 sampling 수가 다르다면 무조건 noramlization을 해주어야지 제대로된 fft 그래프를 그릴 수 있다.
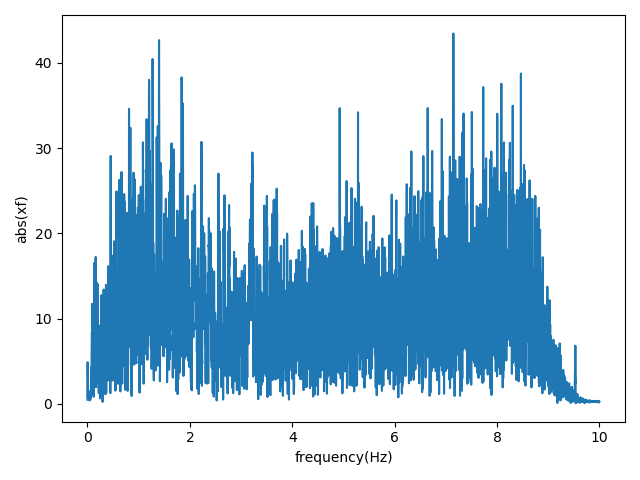

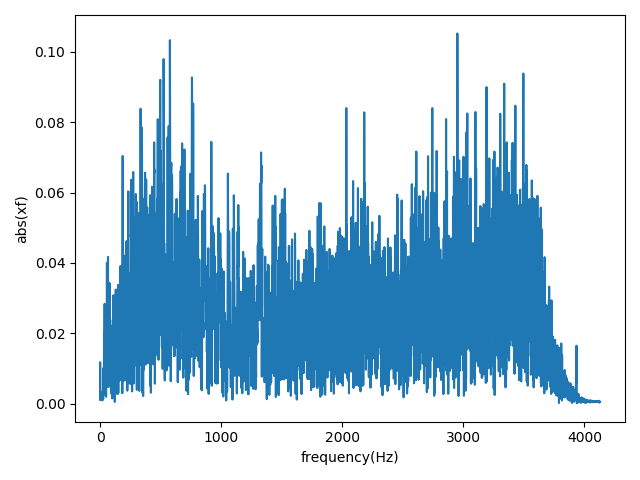
- sampling rate를 고려하지 않을 때는 단순히 data의 length만 고려하기 때문에 적절하지 않다.
16000개 데이터를 samplig rate 변화를 주었을때




- 결론.. sampling rate 자체를 바꾸려면 그냥 data를 축소시키는 방법밖에 없다.
- 단순히 20Hz와 40Hz 데이터를 비교할 수 있는 방법이 없다 . 데이터 축소 밖에 없을 듯
[전체 코드]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
|
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
class seismic_data_arrangement:
def __init__(self):
self.time_data = []
self.x_data = []
self.y_data = []
self.z_data = []
self.data_list = []
def data_arrangement_xdata(self, file_name):
self.read_excel = pd.read_csv(file_name)
self.x_data.append(float(self.read_excel.columns[1]))
for j in range(0, self.read_excel.shape[0]):
# print( read_excel.shape[0])
self.x_data.append(self.read_excel.iloc[j, 1])
return self.x_data
def data_arrangement_ydata(self, file_name):
self.read_excel = pd.read_csv(file_name)
self.y_data.append(float(self.read_excel.columns[2]))
for j in range(0, self.read_excel.shape[0]):
# print( read_excel.shape[0])
self.y_data.append(self.read_excel.iloc[j, 2])
return self.y_data
def data_arrangement_zdata(self, file_name):
self.read_excel = pd.read_csv(file_name)
self.z_data.append(float(self.read_excel.columns[3]))
for j in range(0, self.read_excel.shape[0]):
# print( read_excel.shape[0])
self.z_data.append(self.read_excel.iloc[j, 3])
return self.z_data
def data_arrangement_time_data(self, file_name):
self.read_excel = pd.read_csv(file_name)
self.time_data.append(float(self.read_excel.columns[0]))
for j in range(0, self.read_excel.shape[0]):
# print( read_excel.shape[0])
self.time_data.append(self.read_excel.iloc[j, 0])
return self.time_data
def data_arrangement_data_more_simple(self, file_name, direction='x'):
self.read_excel_init = pd.read_csv(file_name, names=['time', 'x', 'y', 'z'])
self.data_list = self.read_excel_init[direction].values
return self.data_list
class fft_class:
def def_fft(self, fmax, data):
dt = 1/fmax #samplign period ,sampling rate
N = len(data)
#Fourier spectrum
df = fmax / N
self.f = np.arange(0, N) * df
self.xf = np.fft.fft(data) * dt
# self.f = np.arange(0, N)
# self.xf = np.fft.fft(data)
return self.f, self.xf
def def_fft_plot(self, f, xf, data):
N = len(data)
plt.plot(f[0:int(N / 2 + 1)], np.abs(xf[0:int(N / 2 + 1)]))
plt.xlabel('frequency(Hz)');
plt.ylabel('abs(xf)');
plt.show()
def fft_total_data(self, fmax, data):
#여기서는 samplign data의 정보는 없다
#1초에 얼마 2초에 얼마 했느지 정보는 없음 ...
dt = 1 / fmax # samplign period ,sampling rate
n = len(data)
Fs = dt
T = n/Fs
f = np.arange(0, n)
freq = f/T
freq = freq[range(int(n / 2))]
Y = np.fft.fft(data) / n
#Y = Y[range(int(n / 2))]
plt.plot(f[0:int(n / 2 + 1)], np.abs(Y[0:int(n / 2 + 1)]))
plt.xlabel('frequency(Hz)');
plt.ylabel('abs(xf)');
plt.show()
fft_data = np.fft.fft(data)
file_name = '10599863_0_sigma_scale1.csv'
data = seismic_data_arrangement()
#x_data = data.data_arrangement_xdata(file_name)
x_data = data.data_arrangement_data_more_simple(file_name,'x')
y_data = data.data_arrangement_data_more_simple(file_name,'y')
print(x_data)
fft = fft_class()
# f, xf = fft.def_fft(20, x_data)
# fft.def_fft_plot(f,xf,x_data)
f, yf = fft.def_fft(20, y_data)
fft.def_fft_plot(f,yf,y_data)
# fft_data = np.fft.fft(x_data)
# fft.def_fft_plot(fft_data,
fft.fft_total_data(20, y_data)
|
cs |
'Engineering > signal' 카테고리의 다른 글
| 양자역학에 대한 생각와 양자 신호처리 (1) | 2020.06.19 |
|---|---|
| 신호에 대한 이해 (0) | 2020.06.19 |
| 나이퀴스트 이론 Nyquist-Shannon sampling theorem = 샘플링 정리 (0) | 2020.06.19 |
| 신호처리 - 웨이블렛(wavelet) (1) | 2019.10.16 |
| 신호처리 - 푸리에변환 (Fourier transform) (1) | 2019.10.16 |
