티스토리 뷰
1. 웨이블렛(wavelet)
- 국부적으로 존재하는 어떤 하나의 작은 파(wavelet)를 패턴으로 하여 이것을 천이시키거나 확대, 축소의 스케일(scale)을 통하여 임의의 파형으로 표현
- 기본 함수로 sine, cosine 함수 이외에 웨이블릿 모함수 사용
- 웨이블릿은 0을 중심으로 증가와 감소를 반복하는 진폭을 수반한 파도와 같은 진동
- 합성곱(convolution) 기술을 통해 알고 있는 신호와 결합하여, 알려지지 않은 신호로부터 정보를 추출하는데에 사용될 수 있음
- 대표적인 wavelet 변환 기법: Orthonormal Wavelet, Biorthonormal Wavelet, Packet Wavelet, Chirplet Wavelet 등의 변환
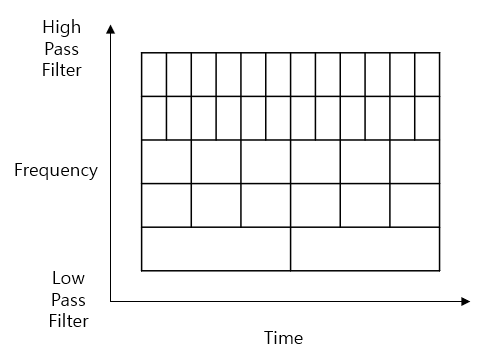
- 고주파수 영역에서는 시간축의 창폭을 조밀하게 하여 시간 영역의 분해능 증가
- 저주파수 영역에서는 시간축의 창폭을 증가시켜 주파수의 분해능 증가
- 웨이블렛 변환은 단시간 푸리에 변환보다 자료를 처리함에 있어서 유연한 해석 가능.

- 웨이블릿 변환에 사용되는 기저함수의 집합은 하나의 기본 웨이블릿 기저함수(mother wavelet basis function)에 대한 시간축 방향으로의 확대 및 축소, 그리고 평행이동을 통해 얻어진다.
- 기본 웨이블릿 기저 함수는 특별한 형태의 밴드(band-pass) 필터로 생각할 수 있다.
- 웨이블릿 변환에서는 주파수 대역이라는 용어대신 스케일(scale)이라는 용어를 주로 사용
- 입력신호에 대한 웨이블릿 변환을 다른 말로 원신호의 시간, 스케일 공간표현이라고도 한다
|
웨이블릿 변환과 푸리에 변환 비교 |
|
|
푸리에변환 |
웨이블릿변화 |
|
어떤 주파수 대역에서든 같은 해상도 |
주파수 대역이 높으면 높은 해상도 이산웨이블릿변환 = 다중 해상도 분석 |
'Engineering > signal' 카테고리의 다른 글
| 양자역학에 대한 생각와 양자 신호처리 (1) | 2020.06.19 |
|---|---|
| 신호에 대한 이해 (0) | 2020.06.19 |
| 나이퀴스트 이론 Nyquist-Shannon sampling theorem = 샘플링 정리 (0) | 2020.06.19 |
| 신호처리 - 푸리에변환 (Fourier transform) (1) | 2019.10.16 |
| python FFT 구현 (0) | 2019.09.11 |
댓글
